Computer Generated Holograms for Cold Atoms: The Story So Far

In recent years, there has been increasing interest in spatially-tailored optical patterns for use in manipulating ultracold neutral atoms. We have developed methods to produce smooth, high-accuracy and multi-wavelength light patterns by engineering the phase of light with a Spatial Light Modulator (SLM).

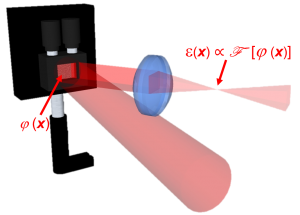
Holographic optical traps allow for the creation of fully arbitrary, complex trapping geometries. An incoming laser beam diffracts off an SLM, acquiring a phase profile from the displayed computer generated hologram (CGH). After subsequent focusing with a lens, the intensity distribution in the Fourier plane of the lens is proportional to the Fourier transform of the phase pattern on the SLM, allowing for dynamic, non-periodic trap configurations.

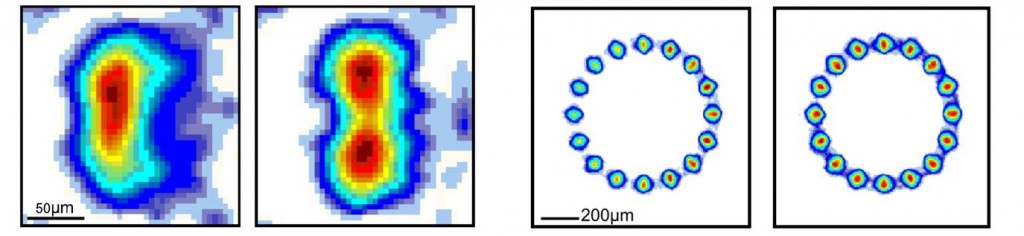
The calculation of phase-modulating holograms is an inverse problem, and is commonly performed by variants of the Gerchberg-Saxton Iterative Fourier Transform Algorithm. As an alternative to this approach, we developed a new method for the generation of holograms based on the direct minimisation of a cost function by a conjugate gradient local search algorithm [1]. Smoothness of the light pattern (important in cold atom experiments to avoid heating the ensemble) is ensured by regional weightings in the cost function used to determine the accuracy of the resultant light pattern. This algorithm offers a high degree of control, as demonstrated by controlling optical vortex formation, and converges even from random initials conditions.

Very recently, we have shown that the approach can be used to control not only the intensity, but also the phase of the light [2].

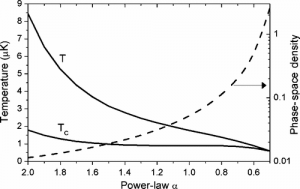
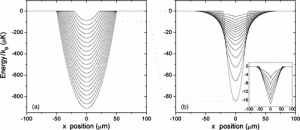
Light patterns are experimentally realised using a single SLM illuminated by up to three overlapped laser beams at 670nm, 780nm and 1064nm. An example of a possible experiment in a holographic optical trap is reversible and efficient formation of Bose-Einstein Condensates in dynamic power-law traps [3].

Furthermore, these traps can be used in quantum simulations, for example when combined with quantum gas microscopes [4]. We have presented SLM-assisted schemes to observe both topological Kondo physics [5] and the Edwards Anderson order parameter of the Bose glass [6].

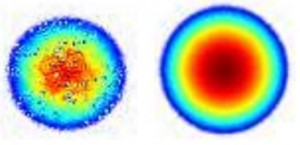
In order to compensate for experimental aberrations, we have developed a simple and robust feedback-enhanced algorithm [7, 8] to improve the accuracy of the light patterns, which reduces the RMS error to the percent level.

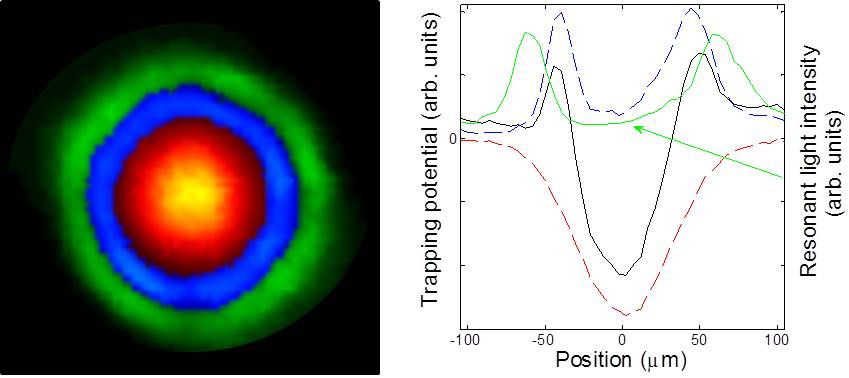
The combination of regional calculation and feedback algorithm is further used to generate multi-wavelength holographic light patterns using just a single SLM [9], where the light profile of each wavelength is independently controlled.

[1] T. Harte, G. D. Bruce, J. Keeling and D. Cassettari, Opt. Express 22, 26548-26558 (2014)
[2] D. Bowman, T. L. Harte, V. Chardonnet, C. De Groot, S. J. Denny, G. Le Goc, M. Anderson, P. Ireland, D. Cassettari and G. D. Bruce, Opt. Express  25 11692-11700 (2017)
[3] G. D. Bruce, S. L. Bromley, G. Smirne, L. Torralbo-Campo and D. Cassettari, Phys. Rev. A 84, 053410 (2011)
[4] E. Haller, J. Hudson, A. Kelly, D. A. Cotta, B. Peaudecerf, G. D. Bruce and S. Kuhr,
Nature Phys. 11, 738-742 (2015)
[5] F Buccheri, G D Bruce, A Trombettoni, D Cassettari, H Babujian, V E Korepin and P Sodano, New J. Phys.  18 075012 (2016)
[6] S. J. Thomson, L. S. Walker, T. L. Harte and G. D. Bruce, Phys. Rev. A 94, 051601(R) (2016)
[7] G. D. Bruce, J. Mayoh, G. Smirne, L. Torralbo-Campo and D. Cassettari, Phys. Scr. T143 014008 (2011)
[8] G. D. Bruce, M. Y. H. Johnson, E. Cormack, D. A. W. Richards, J. Mayoh and D. Cassettari, J. Phys. B 48 115303 (2015)
[9] D. Bowman, P. Ireland, G. D. Bruce and D. Cassettari, Opt. Express 23, 8365-8372 (2015)